
Plasticity, Collapse and Fatigue
If loading causes regions in a structure to become plastic (i.e. exceed the yield stress) an analysis which includes a material with post-yield stiffness is required to evaluate the plastic stresses. A simple example is illustrated below. A linear analysis in which only the Young’s Modulus (E) is included will substantially overestimate such plastic stresses and a separate value of post-yield stiffness (often noted as H) is required. Setting a reliable value for H is often problematic but a value many orders less than E (and sometimes zero – see previous articles) is often used.
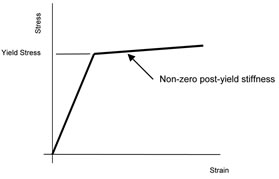
Stresses acting over cross sections can be perceived as a reaction to the applied loads on that section. While a structure is still mainly elastic, increases in load will cause the stresses to increase in proportion. Eventually, small regions of plasticity will initialise at stress concentrations (or notches). Because of the reduced stiffness of these plastic regions, as the applied load is increased, stresses increase much less compared with the surrounding non-yielded material. Furthermore, the elastic, stiffer surrounding regions control the deformation of the smaller and less stiff plastic regions. In other words, initial plastic regions are displacement or strain controlled, by the surrounding regions. Although not literally true, imagining an initial yielded region as a portion of relatively softer material may help to visualise how it is affected by increases in applied load.
As well as giving a much-improved set of stress results immediately post-yield, plasticity analysis can provide an insight into how a multiply-connected (multiple load-path) structure fails (collapses), as the load is increased. Previous ‘Knowledge Base’ articles have discussed aspects of such methods to determine structural collapse.
Clearly, a load that results in structural collapse can be applied only once. However, lower loads, that still exceed the yield stress, can be repeatedly applied before failure occurs (termed cyclic, fatigue or reversed loading). A plastic material model is also required in the analysis of such cases. (In pressure vessel terminology this is termed shakedown and ratchetting.) In these cases, for a given value of load, the stress at any point within the plastic regions during unloading is different to that during loading. This implies a hysteresis loop of cyclic stress, as illustrated above (which shows the load and stress as being fully reversed, i.e. having a zero mean).
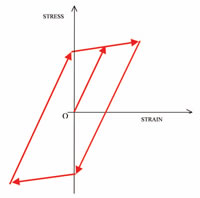
At each point in the structure where the yield stress has been exceeded, hysteresis loops of various sizes will be traversed as the load is repeatedly applied. Prior to the advent of plasticity in FEA, there was no generally applicable procedure for establishing whether a given cyclic load acting on a given structure will cause a continual growth of the plastic regions and the hysteresis loops, resulting in eventual collapse (ratchetting), or whether the regions will eventually stop growing and all the hysteresis loops become stable (shakedown).
Even though a cyclic load can shakedown the structure to a stable stress state, this does not imply that the structure can sustain this cyclic load for an infinite number of cycles. Repeated loading of this sort will cause the material to sustain fatigue damage, so that some regions experiencing the same repeated value of stress, while sustainable in the short term, will eventually start to rupture.
Fatigue damage is not manifested as a change in the material stiffnesses used in the FE material model and is therefore considered as a separate analysis or post-processing step, after the main solution. Note that fatigue damage is caused by repeated cyclic stressing, whether the yield stress is exceeded or not, and is a distinct phenomenon from ratchetting or plastic collapse. It is relevant to all cyclic load scenarios





