The Importance of Mesh Convergence

This two-part article describes what might be one of the most overlooked issues that affect accuracy, namely; mesh convergence. This refers to the smallness of the elements required in a model to ensure that the results of an analysis are not affected by changing the size of the mesh. We have encountered occasions where mesh size is just accepted as a historical legacy that cannot be changed, and no knowledge of its affect on accuracy is available. This is bad practice.

This article is directly applicable to static stress analysis. Whilst the issue of mesh size is important in all analyses, there are other issues that affect the selection of an appropriate element size in more advanced analyses. It relates to the majority ‘h element’ programs; ‘p element’ programs (e.g. Pro Mechanica) converge on a result in the solution process and, to a large extent, are not dependent on element size.

How to do a Convergence Study

The Convergence Curve

The formal method of establishing mesh convergence requires a curve of a critical result parameter (typically some kind of stress) in a specific location, to be plotted against some measure of mesh density. At least three convergence runs will be required to plot a curve which can then be used to indicate when convergence is achieved or, how far away the most refined mesh is from full convergence. However, if two runs of different mesh density give the same result, convergence must already be achieved and no convergence curve is necessary.

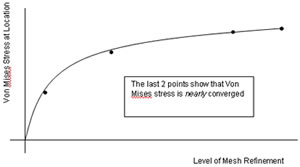
Figure 1 – a 4 point convergence curve

Local Mesh Refinement

In theory, for each successive level of mesh refinement in the convergence study, all elements in the model should be split in all directions. While the latter requirement is important, it is not necessary to carry this out on the whole model: St Venant’s Principle implies that local stresses in one region of a structure do not affect the stresses elsewhere. From a physical standpoint then, we should be able to test convergence of a model by refining the mesh only in the regions of interest, and retain the unrefined (and probably unconverged) mesh elsewhere. We should also have transition regions, from coarse to fine meshes, suitably distant from the region of interest (at least 3 elements away for linear elements).

Boundary Geometry – a Related Effect

A common influence on stress results when using linear (straight sided) elements to represent a curved surface or edge is that the geometry of the boundary will be better represented, as the mesh is refined. This is a modelling or geometry effect, different to mesh convergence, which is numerical. It is worth being aware of the distinction between these two affects.

Meshing Strategy

The idea of using only local mesh refinement for a convergence study can be extended. If a model is required to produce accurate stresses only at certain regions of interest, the role of all elements away from these regions is one of only representing geometry and transmitting load. This demands a much lower level of mesh refinement than for accurate stress prediction. Thus, these elements can be considerably larger, subject to the constraints of permitting both reasonable quality transitions and geometry representation.

Using larger elements away from regions of interest in a model is common practice but a more subtle point is, providing they don’t misrepresent the geometry and suitable mesh transitions can be carried out; these elements can be considerably larger than those in regions of interest, without jeopardising accuracy. Contrast this as a meshing strategy against that of filling an entire model with small, high-quality elements, to improve ‘overall’ accuracy. This latter approach is inefficient and unlikely to improve accuracy in static stress analysis with an implicit code.

Summary

• Every department should have some basic data on mesh convergence for their models.
  
• A number of runs of a model with increasing levels of mesh refinement in the areas of interest can be used to demonstrate mesh convergence.
  
• Element sizes distant from a region do not significantly affect the results in that region, providing they do not grossly misrepresent the distant geometry.

Extending the Convergence Study to Other Models

If one model has been subject to a convergence study, as described in the first article, then it would be logical to argue that the corresponding region in a model of a ‘similar’ structure, with the same level of mesh refinement, would have the same level of accuracy. This is true, providing the ‘similarity’ of models includes similarity in stress gradients.

Often, strengthening a region of a structure can attract more load and produce higher stresses in fillets or other features, requiring careful detail design and analysis. The strengthened structure, in this case, is not ‘similar’ to the previous design in that it will have higher stress gradients, requiring an increase in mesh density in this region, to give comparable accuracy with analysis of the previous design. This is especially important as the stresses tend towards the limiting strength of the material, and become critical to the acceptance of the new design.

Even without design changes to the structure, a simple increase in load magnitude means that stress gradients will be increased in certain regions. Although the accuracy as a percentage of peak stress will not change, the accuracy relative to the yield stress of the material will be reduced, unless the mesh is refined.

Examples of Bad Practice

Using Element Size as a Measure of Convergence

In light of the previous discussion, it will be obvious that assuming a mesh is convergent for stress just because it has the same element size as a converged mesh in a non-similar model, or in a different location in a similar model, is not valid.

Stress accuracy will depend on element size to some extent, but the element’s proximity to a stress concentration or the variation of the load in the structure in the region of interest is more important.

A Common Case of Ignoring Convergence

The figure opposite shows a 2D or 3D mesh region, representing an internal corner. No radius is modelled. An internal corner with zero radius like this could have an infinite theoretical stress if made from a perfectly elastic material. This is not to do with any numerical effects of FEA but because the stress concentration in most situations is infinite for this geometry.

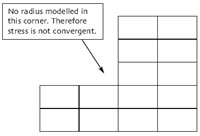
As the mesh is refined, the stress will increase without limit. Thus, the stresses predicted by an FE analysis of a fillet modelled in this way is only dependant on the size of the elements and has nothing to do with any real values that might occur there.

Quite often, sensible stresses can be predicted from representing an internal fillet in this way but that doesn’t mean they are valid; the actual radius specified in the drawing must be represented with a suitable number of elements spaced around the fillet, to achieve a predictable elastic stress. (There could be serious implications if the drawing specifying this feature does not include a minimum radius.)

Summary

• Avoid using element size alone as an indicator of convergence.
  
• Results of a local convergence study can only be extended to corresponding locations in structurally similar models, with similar loadings.
  
• If the load magnitude increases significantly, the accuracy relative to a fixed allowable stress will reduce.
  
• Do not model critical internal fillets as shown in the figure above, since they cannot predict true stresses.

Go to the next Knowledge Base article: Fundamentals of Numerical Techniques for Static, Dynamic and Transient Analyses or go back to Knowledge Base article series list